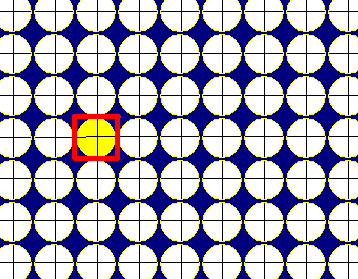
정사각형 테셀레이션
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
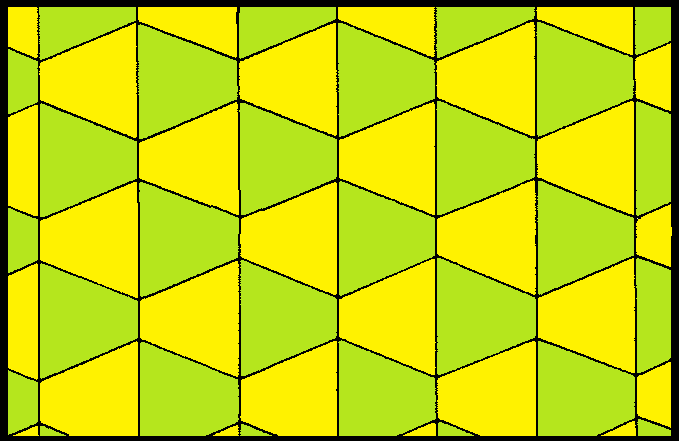
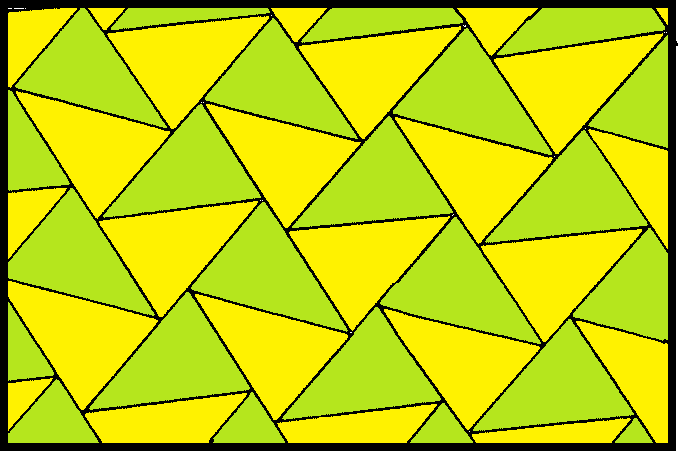
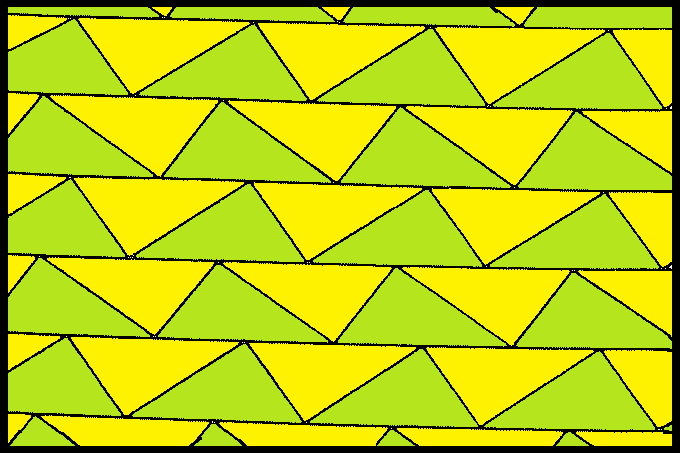
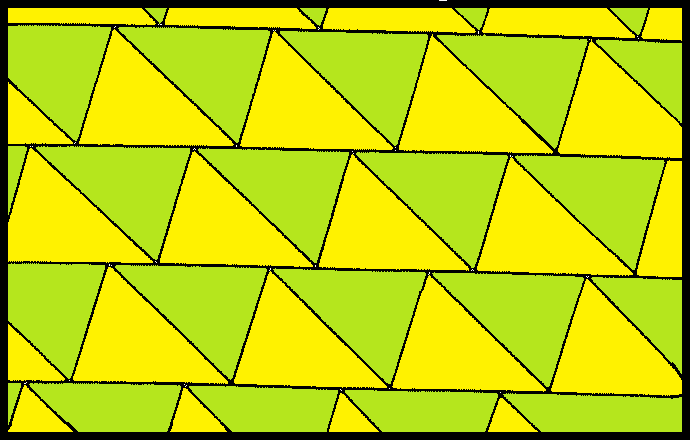
정사각형 테셀레이션은 평면을 정사각형으로 완전히 덮는 규칙적인 타일링을 의미한다. 이 타일링은 9가지의 균일 색칠이 가능하며, 대칭성에 따라 다양한 패턴으로 분류될 수 있다. 또한, 정다면체 및 쌍곡면 테셀레이션과 밀접한 관련이 있으며, 위토프 구성을 통해 3가지 위상적으로 구분되는 형태의 고른 테셀레이션을 생성할 수 있다. 정사각형 타일링은 원 채우기에도 활용되어 채우기 밀도가 π/4이며, 4가지 균일 색칠이 가능하다. 복소 정 무한각형과도 관련이 있으며, 한국의 전통 건축 및 문양에도 활용된다.
더 읽어볼만한 페이지
- 정다각형 타일링 - 정삼각형 테셀레이션
정삼각형 테셀레이션은 평면을 정삼각형으로 빈틈없이 채우는 구조로, 슐레플리 기호 {3,6}으로 표현되며, 다양한 수학적 개념 및 다른 삼각형 테셀레이션과 연관되어 여러 분야에서 활용된다. - 정다각형 타일링 - 정다각형 테셀레이션
정다각형 테셀레이션은 평면을 정다각형으로 채우는 기하학의 한 분야이며, 정규, 준정규, k-균일 타일링 등으로 분류된다. - 다면체 - 마름모구십면체
마름모구십면체는 깎은 정이십면체에 각뿔을 붙여 만든 다면체이며, 넓은 마름모 60개와 좁은 마름모 30개로 구성되고 좁은 마름모는 황금비의 제곱과 관련된 대각선 비율을 가지며 최적 충전율은 약 0.7947이다. - 다면체 - 삼각쌍뿔
삼각쌍뿔은 6개의 정삼각형 면, 5개의 꼭짓점, 9개의 모서리를 가진 존슨 다면체이자 델타다면체로, 두 정사면체를 밑면끼리 결합한 형태이며, 분자 기하학, 색채 이론 등 다양한 분야에 응용된다.
2. 균일 색칠
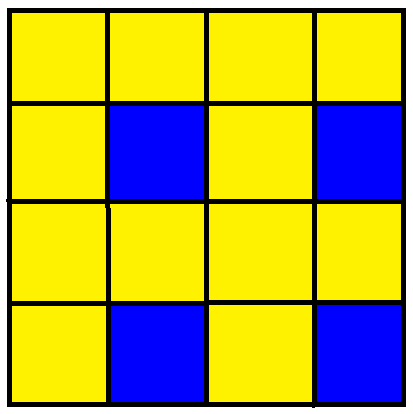
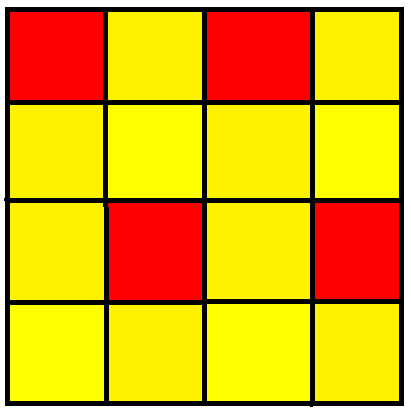
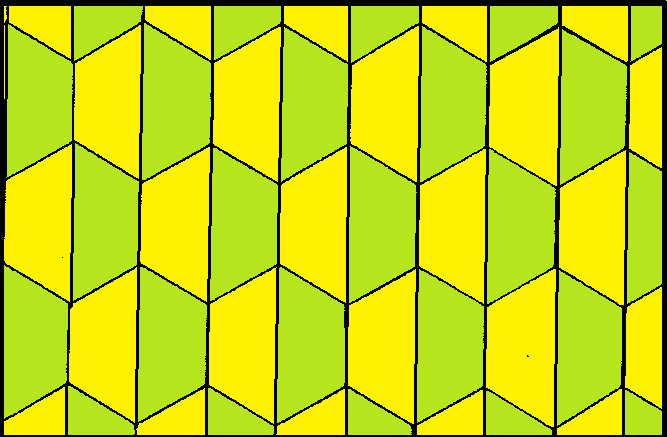
사각형 타일링은 다양한 방식으로 색칠될 수 있으며, 이 중 9가지의 구분되는 균일 색칠이 존재한다. 각 색칠은 꼭짓점 주변의 사각형 색깔에 따라 1111, 1112(i), 1112(ii), 1122, 1123(i), 1123(ii), 1212, 1213, 1234와 같이 표현된다. 여기서 (i)는 단순 반사 대칭을, (ii)는 미끄럼 반사 대칭을 가진다.
1213은 1112i로, 1234는 1123i로, 1123ii는 1112ii로 색칠을 줄여 같은 대칭 영역으로 볼 수 있다.
2. 1. 대칭성에 따른 분류
정사각형 타일링에는 9가지의 균일 색칠이 있다. 꼭짓점 주변 사각형의 색깔을 숫자로 나타내면 1111, 1112(i), 1112(ii), 1122, 1123(i), 1123(ii), 1212, 1213, 1234와 같다. 여기서 (i)는 단순 반사 대칭을, (ii)는 미끄럼 반사 대칭을 갖는다.1213은 1112i로, 1234는 1123i로, 1123ii는 1112ii로 색칠을 줄여 같은 대칭 영역으로 볼 수 있다.
정사각형 타일링은 정다면체 및 다른 테셀레이션과 관련이 깊다.
3. 관련 다면체와 테셀레이션
이 테셀레이션은 정팔면체에서 시작해 슐레플리 기호 {n,4}를 가지는, 꼭짓점에 면이 네 개 있는 정다면체 및 테셀레이션 배열과 위상적으로 연관되어 있다.
하위 섹션에서 이미 자세히 다루고 있으므로, 여기서는 간략하게만 언급한다.
3. 1. 정다면체와의 관계
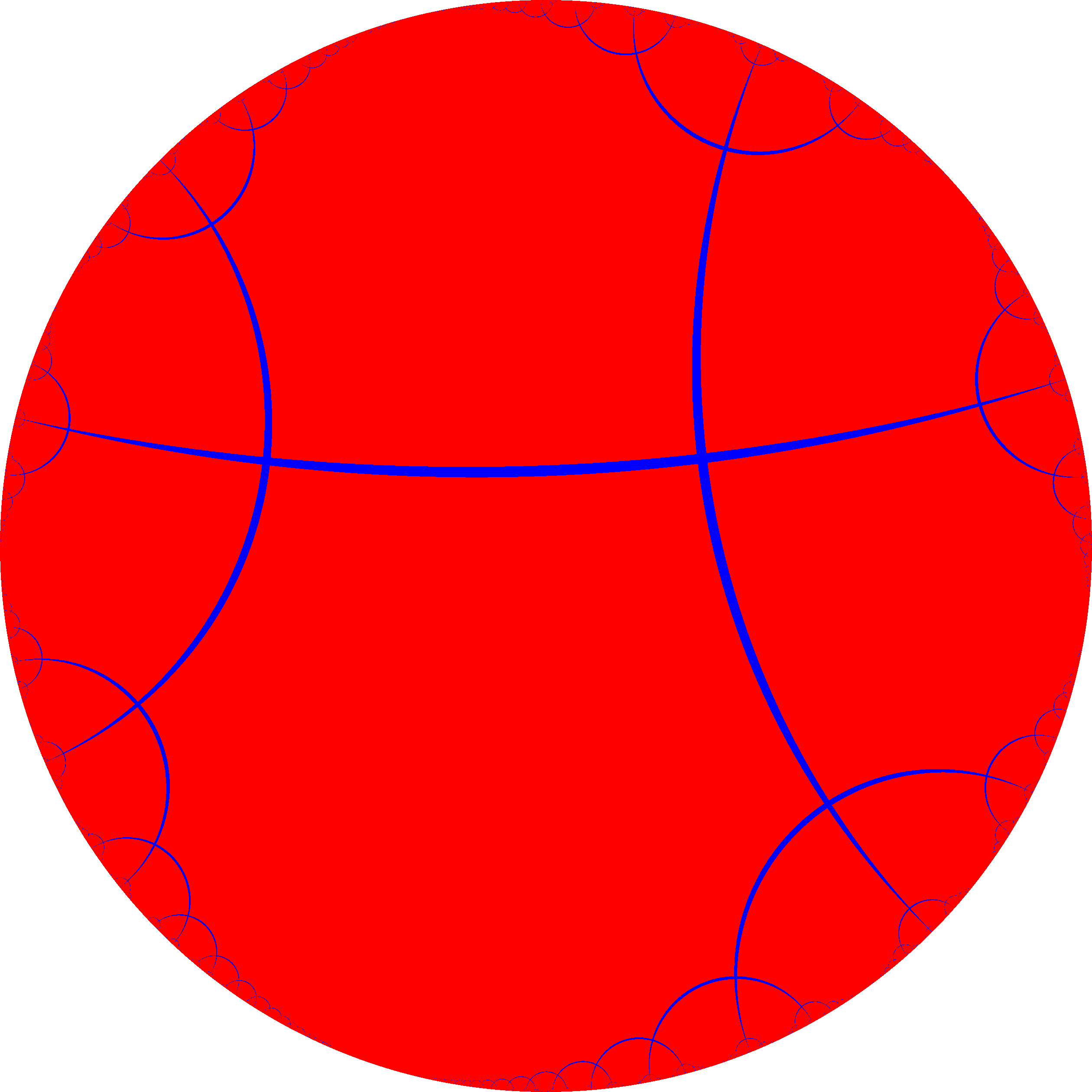
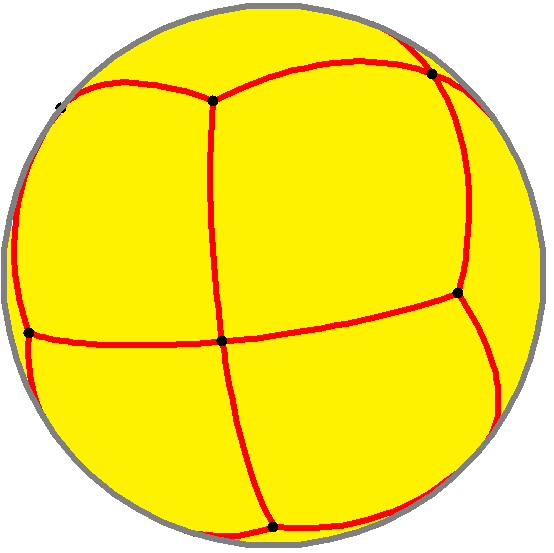
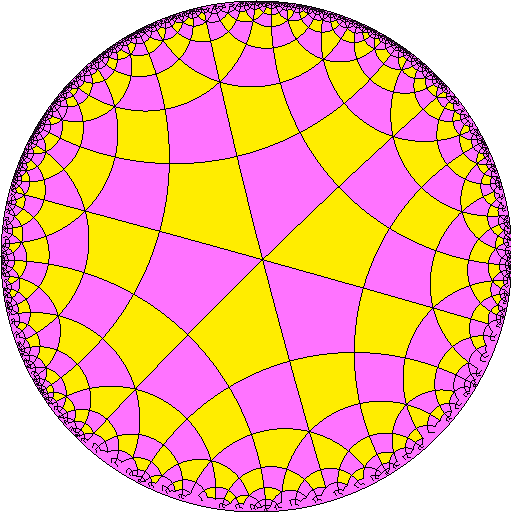
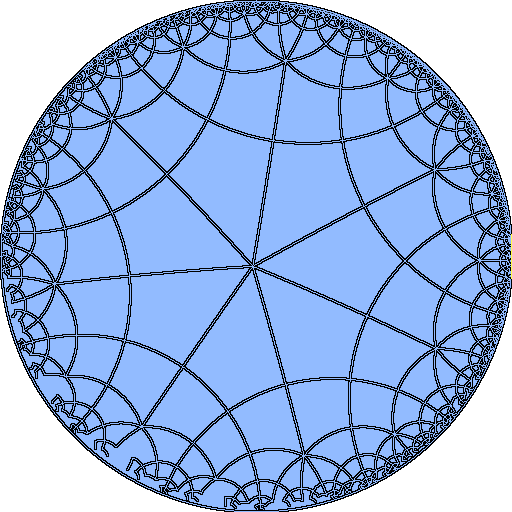
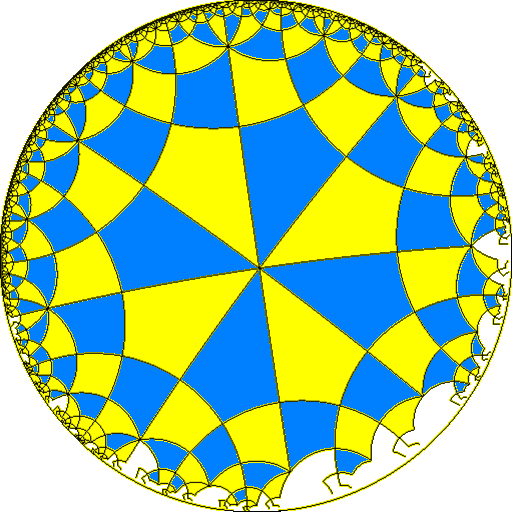
이 타일링은 꼭짓점 도형이 *n*4인 정다면체 및 쌍곡면으로 확장된 정다각형 타일링 수열의 일부와 위상적으로 관련되어 있다. 슐레플리 기호는 {4, p}이며, p=3, 4, 5,...이다.
또한, 꼭짓점에 면이 네 개 있는 정다면체와 테셀레이션 배열의 일부와도 위상적으로 연관되어 있다. 이 수열은 정팔면체에서 시작하여 슐레플리 기호 {n,4}를 가지며, n이 무한으로 갈 때 쌍곡 평면이 된다.[1]
3. 2. 꼭짓점 배열에 따른 분류
{n,4}{2,4}
{3,4}
{4,4}
{5,4}
{6,4}
{7,4}
{8,4}
{∞,4}